flowchart LR A(Input Variations) --> B(Perturbed Data) A --> C(Unperturbed Data) B --> D(Adversarial Perturbation) B --> E(Non-adversarial Perturbation) C --> F(Out-of-distribution) C --> G(Outlier & Infrequent Behaviour) C --> H(Concept Drift)
🧑💻 Zhipeng “Zippo” He @ School of Information Systems
Queensland University of Technology
Comfirmation Seminar
March 15, 2023
Research Background
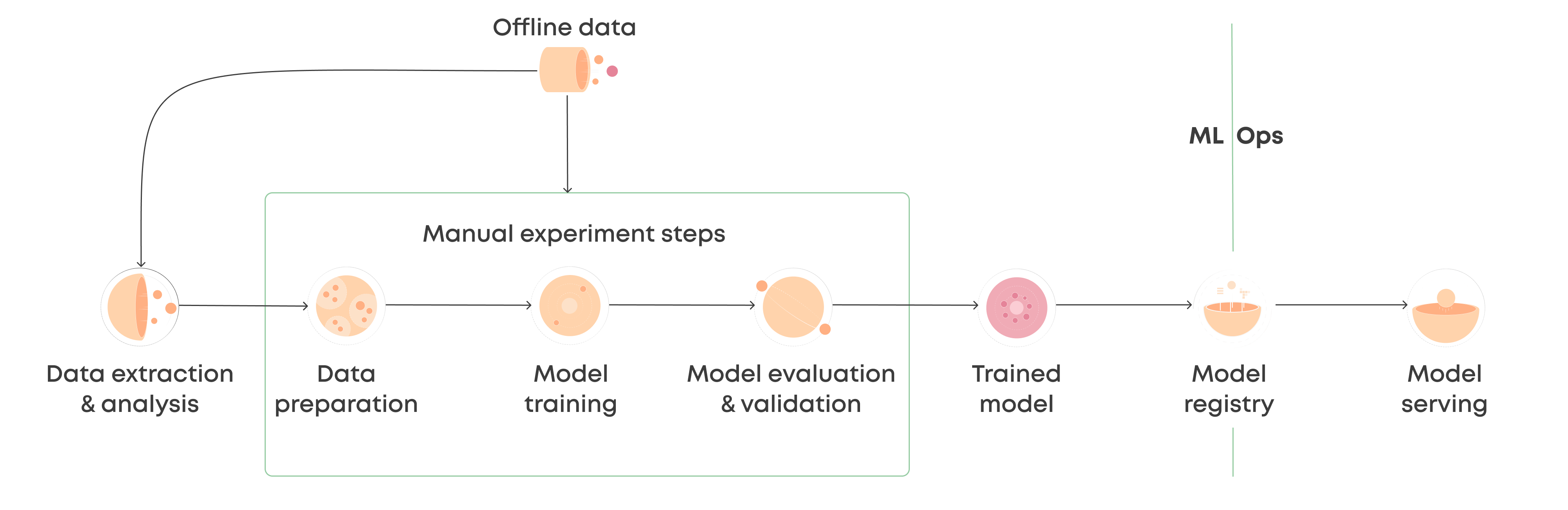
In philosophy of science (Woodward 2006), the closest notion of robustness against data science is:
Inferential Robustness
For example,
Y is robust = Y is the inference from a given D, and Y remains invariant to alternative assumptions in D.
In machine learning, Y = Predictive models, D = input
In machine learning, robustness refers to the ability of a model to:
perform well on unseen or new data
variations in the input
A robust model is not overly sensitive to perturbation in the input data, such as adversarial examples, and it can also generalise well against distributional variations.
flowchart LR A(Input Variations) --> B(Perturbed Data) A --> C(Unperturbed Data) B --> D(Adversarial Perturbation) B --> E(Non-adversarial Perturbation) C --> F(Out-of-distribution) C --> G(Outlier & Infrequent Behaviour) C --> H(Concept Drift)

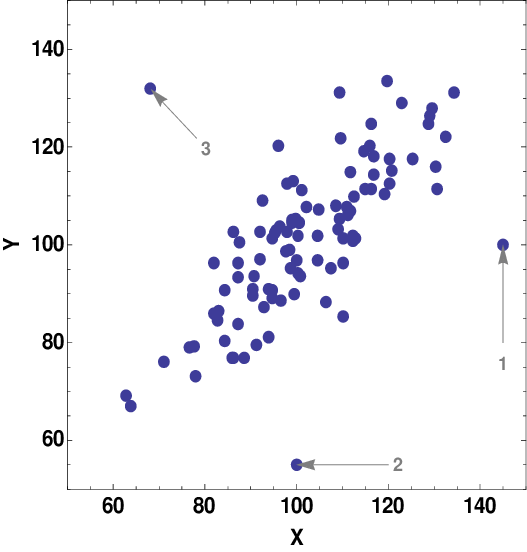
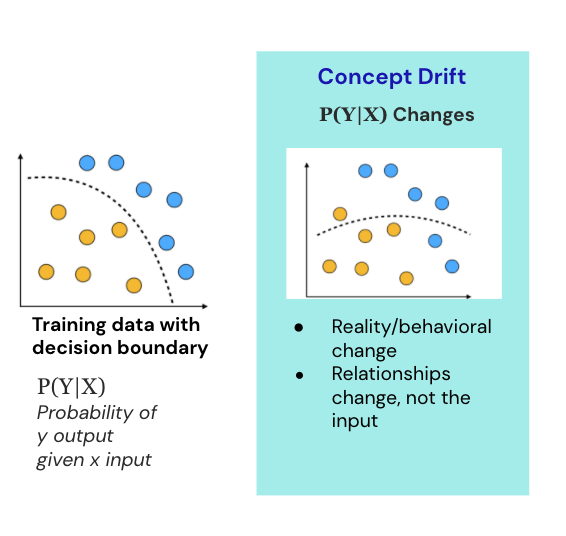
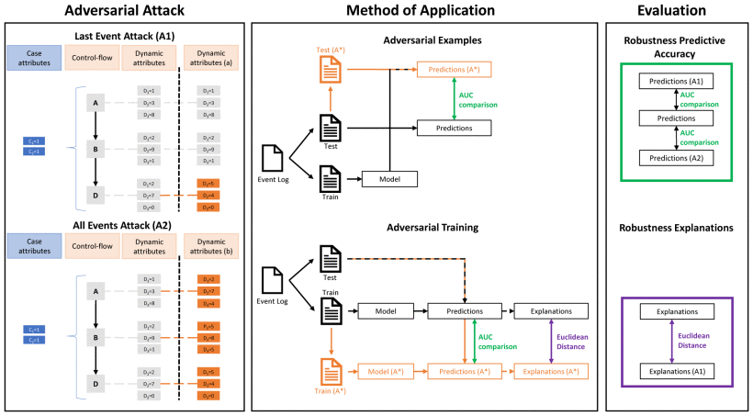
An adversarial attack is a method to generate adversarial examples.
Adversarial examples are specialised inputs created with the purpose of confusing a neural network, resulting in the misclassification of a given input. These notorious inputs are indistinguishable to the human eye but cause the network to fail to identify the contents of the image. (Goodfellow, Shlens, and Szegedy 2015)

Attack Attacks
\[ \DeclareMathOperator*{\argmin}{arg\,min} $\newcommand{\one}{\unicode{x1d7d9}}$ "\uD54F" \]
Given a machine learning classifier \(f: \mathbb{X}\to \mathbb{Y}\) mapping data instance \(\boldsymbol{x} \in \mathbb{X}\) to label \(y \in \mathbb{Y}\), finding adversarial examples can be seen as an optimisation problem and formalised as: \[ \begin{gathered} \argmin_{\boldsymbol{x}^{adv}} [ d(\boldsymbol{x},\boldsymbol{x}^{adv})+\lambda\cdot d^\prime (f(\boldsymbol{x}),f(\boldsymbol{x}^{adv})) ] \\ \text{such that } f(\boldsymbol{x})\neq f(\boldsymbol{x}^{adv}), \end{gathered} \]
where \(\boldsymbol{x}\) is the original input data instance and \(\boldsymbol{x}^{adv}\) represents an adversarial example. Distance functions \(d\) and \(d^\prime\) are utilised to constrain the smallest changes on inputs while outputs are misclassified.
Confidence Reduction
Nontargeted Misclassification
Targeted Misclassification
Source/Target Misclassification
Confidence Reduction
Nontargeted Misclassification
Targeted Misclassification
Source/Target Misclassification
White-Box Attacks
Grey-Box Attacks
Black-Box Attacks
Image (unstructured):
Tabular (structured):


Inconsistent feature ranges and feature types
Missing or complex irregular spatial dependencies exist in correlation
Information loss may happen when pre-processing features with dependency
Changing a single feature can entirely flip a prediction on tabular data
Long-term feature dependencies
Variable-length inputs
Control-flow constraints
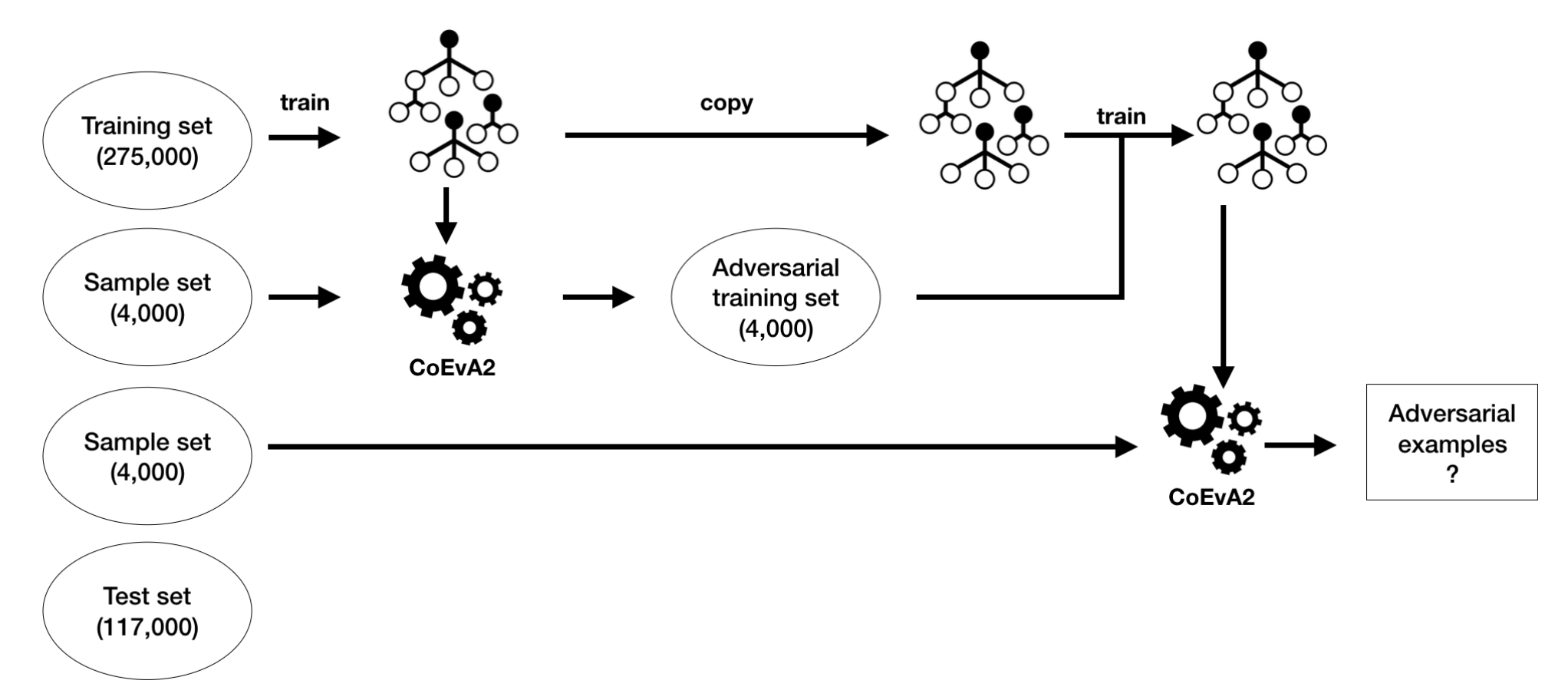
Research Questions
Researchers have been working on developing methods to make these models more robust to adversarial attacks, but this work has mainly focused on unstructured data. However, some researchers have rarely investigated adversarial robustness for structured data.
How can one construct predictive models that are robust to adversarial attacks for both tabular data and sequential data?
RQ1: What characteristics can be applied to determine the success of adversarial attacks on structured data?
RO1: Identify the set of characteristics of successful adversarial attacks on structured data.
RQ2: How to evaluate the characteristics of adversarial attacks (identified in RQ1) on structured data?
RO2: Develop an evaluation framework to benchmark adversarial attacks on structured data.
RQ3: What techniques can be utilised to reduce the impact of adversarial attacks, as identified in RQ2, on the robustness of predictive models for structured data?
RO3: Design defence algorithms into predictive models against adversarial attacks for structured data.
Research Plan
Phase I: Background research, problem definition, and literature review
Phase II: Evaluation of adversarial attack techniques (Iterative)
Phase III: Development and evaluation of defence techniques (Iterative)
Phase IV: Tool implementation and thesis write up
Progress to Date
Phase 1.2
Effectiveness
Imperceptibility
Transferability
Phase 1.2
Effectiveness
Imperceptibility
Transferability
Phase 2.1
Natural Accuracy & Robust Accuracy (Yang et al. 2021).
\[ \begin{gathered} \text{Natural Accuracy}= \frac{1}{n}\sum_{i=1}^{n}\one(f(\boldsymbol{x}_i)=y_i) \\ \text{Robust Accuracy}= \frac{1}{n}\sum_{i=1}^{n}\one(f(\boldsymbol{x}^{adv}_i)= y_i) \end{gathered} \]
Phase 2.1
The success rate of an adversarial attack is the percentage of input samples that were successfully manipulated to cause misclassification by the model.
\[ \begin{gathered} \text{Untargeted Success Rate} = \frac{1}{n}\sum_{i=1}^{n}\one( \boldsymbol{x}^{adv})\neq f(\boldsymbol{x}_i)) \\ \text{Targeted Success Rate} = \frac{1}{n}\sum_{i=1}^{n}\one( \boldsymbol{x}^{adv})= y^*_i) \end{gathered} \]
Phase 2.1
A good adversarial example is expected to perturb fewer features that will result in changing the model’s prediction.
Here, I adapt \(\ell_0\) norm (Croce and Hein 2019) to tabular data as sparsity metric, which measures the number of changed features in an adversarial example \(\boldsymbol{x}^{adv}\) compared to the original input vector \(\boldsymbol{x}\).
\[ Spa(\boldsymbol{x}^{adv}, \boldsymbol{x})=\ell_0(\boldsymbol{x}^{adv}, \boldsymbol{x})=\sum_{i=1}^{n}\one( x^{adv}_i-x_i) \]
Phase 2.1
A good adversarial example is expected to introduce minimal perturbation, which can be obtained as the smallest distance to the original feature vector.
In addition to \(\ell_p\) norm that is commonly used for measuring perturbation distance, I also adapt the distance metrics used to evaluate the quality of counterfactual explanations for tabular data (Mazzine and Martens 2021).
For all proximity metrics, the lower value is , the more imperceptible is
Phase 2.1
Phase 2.1
Phase 2.1
Perturbed vectors should be as similarly as possible to the majority of original vectors.
Phase 2.1
Phase 2.1
Phase 2.2
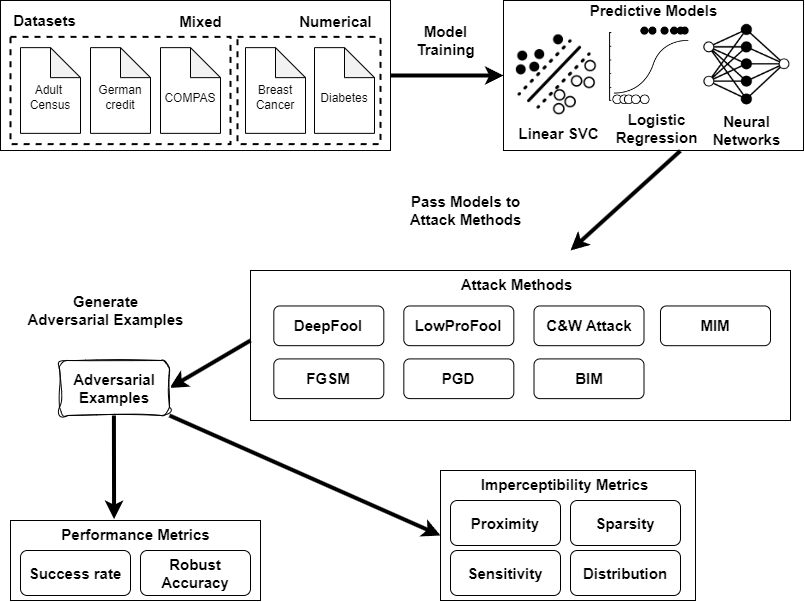
Phase 1.3 & 2.2
Selection Criteria:
Gradient-based: FGSM, BIM, MIM, PGD
Decision boundary-based: DeepFool, LowProFool
Optimization-based: C&W attack
Phase 2.2
Selection Criteria:
Logistic Regression (LR)
Support Vector Machine (SVM)
Multilayer Perceptrons (MLP)
| Dataset | Data Type | Total Inst. |
Train/Test Set |
Total Feat. |
Cate. Feat. |
Num. Feat. |
Enc.Cate. Feat. |
|---|---|---|---|---|---|---|---|
| Adult | Mixed | 32651 | 26048/6513 | 12 | 8 | 4 | 98 |
| Breast | Num | 569 | 455/114 | 30 | 0 | 30 | 0 |
| COMPAS | Mixed | 7214 | 5771/1443 | 11 | 7 | 4 | 19 |
| Diabetes | Num | 768 | 614/154 | 8 | 0 | 8 | 0 |
| German | Mixed | 1000 | 800/200 | 20 | 15 | 5 | 58 |
| Datasets | LR | SVM | MLP |
|---|---|---|---|
| Adult | 0.8524 | 0.8532 | 0.8521 |
| German | 0.8125 | 0.8125 | 0.7969 |
| COMPAS | 0.7933 | 0.7976 | 0.8089 |
| Diabetes | 0.7578 | 0.7578 | 0.7266 |
| Breast Cancer | 0.9844 | 0.9844 | 0.9688 |
There is a trade-off between imperceptibility and effectiveness.
Optimisation-based attacks should be the preferred methods for tabular data.
Overall, C&W \(\ell_2\) attack obtains the best balance between imperceptibility and effectiveness.
C&W attack is designed to optimise a loss function that combines both the perturbation magnitude with distance metrics and the prediction confidence with objective function:
\[ \argmin_{\boldsymbol{x}^{adv}} \Vert\boldsymbol{x}-\boldsymbol{x}^{adv}\Vert_p + c\cdot z(\boldsymbol{x}^{adv}) \]
Adding sparsity as a term in the optimisation function is important for adversarial attacks on structured data.
Future Work
Phase 2.1
Introduce domain knowledge into the evaluation of imperceptibility.
Immutability
Feasibility
Phase 2.1
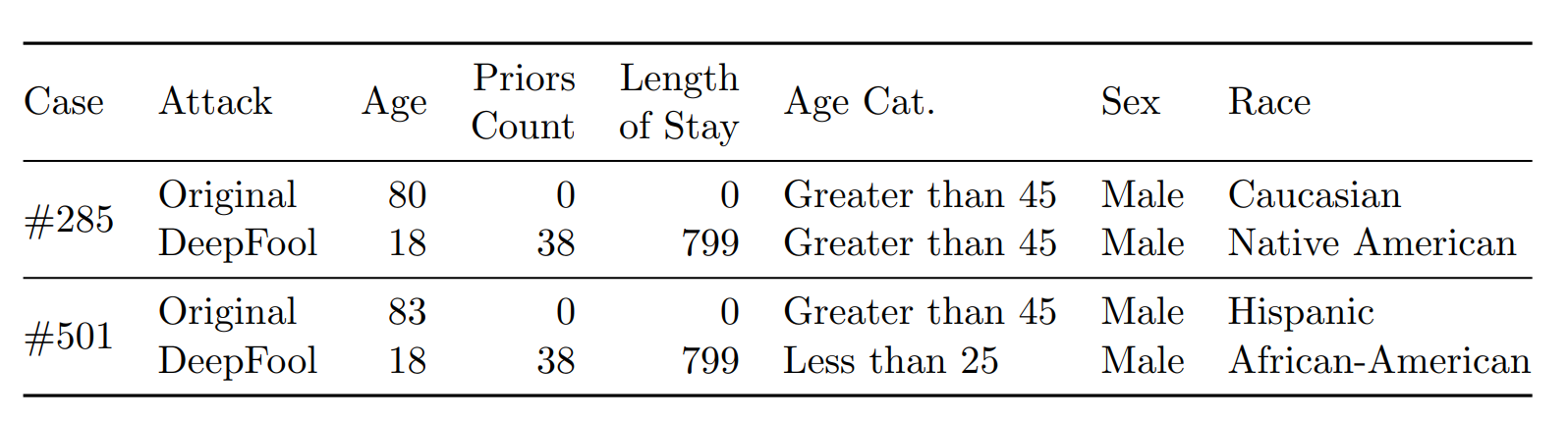
Phase 2.1
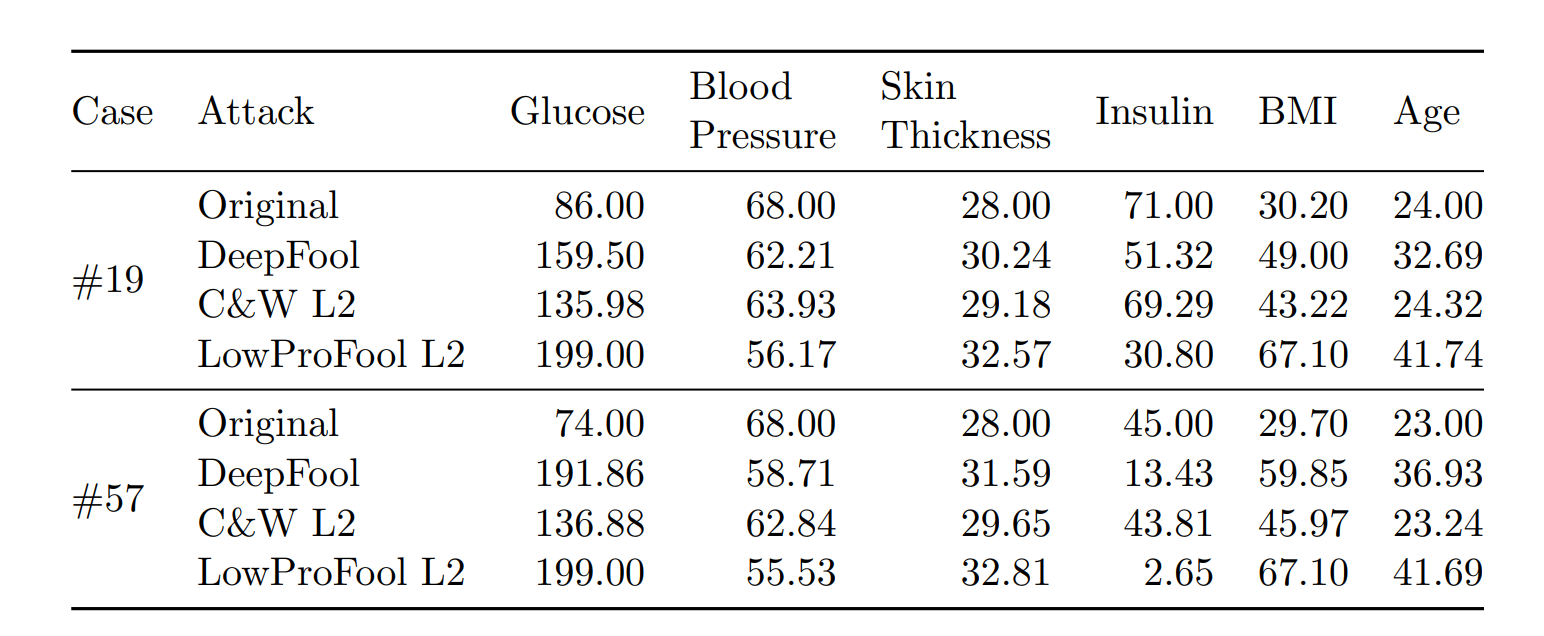
Phase 2.2 & 2.3
Extension of benchmark
Phase 3
Adversarial Defences
Imperceptibility Metric & White-box Attack Evaluation on tabular data
The comprehensive adversarial attack benchmark on tabular data will submit to Q1 journal.
CORE ranking A* Conferences
CORE ranking A Conferences
Scimago Q1 Journals
Thank you!
